How to generate a torus in MATLAB ?
In geometry, a torus (plural tori) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution.
MATLAB Program:
Output:
MATLAB Program:
function [xx,yy,zz] = torus(r,n,a)
%TORUS Generate a torus
% torus(r,n,a) generates a plot of a torus
with central
% radius
a and lateral radius r. n controls the number
% of facets on the surface. These input variables are optional
% with defaults r = 0.5, n = 20, a = 1.
%
% [x,y,z] = torus(r,n,a) generates three
(n+1)-by-(2n+1)
% matrices so that surf(x,y,z) will produce
the torus.
if nargin < 3, a = 1; end
if nargin < 2, n = 20; end
if nargin < 1, r = 0.5; end
theta = pi*(0:2*n)/n;
phi = 2*pi*(0:n)'/n;
x = (a + r*cos(phi))*cos(theta);
y = (a + r*cos(phi))*sin(theta);
z = r*sin(phi)*ones(size(theta));
if nargout == 0
surf(x,y,z)
ar = (a + r)/sqrt(2);
axis([-ar,ar,-ar,ar,-ar,ar])
else
xx = x; yy = y; zz = z;
end
Output:





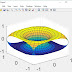


























No comments