Romberg integration algorithm using MATLAB
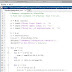
MATLAB PROGRAM:
% Romberg integration algorithm
% Find the integral of y=sin(x) from 0 to pi.
f = @(x) sin(x);
a = input('Enter lower limit, a: ');
b = input('Enter upper limit, b: ');
n = input('Enter no. of subintervals, n: ');
h = b-a;
r = zeros(2,n+1);
r(1,1) = (f(a)+f(b))/2*h;
fprintf('\nRomberg integration table:\n');
fprintf('\n %11.8f\n\n', r(1,1));
for i = 2:n
sum = 0;
for k = 1:2^(i-2)
sum = sum+f(a+(k-0.5)*h);
end
r(2,1) = (r(1,1)+h*sum)/2;
for j = 2:i
l = 2^(2*(j-1));
r(2,j) = r(2,j-1)+(r(2,j-1)-r(1,j-1))/(l-1);
end
for k = 1:i
fprintf(' %11.8f',r(2,k));
end
fprintf('\n\n');
h = h/2;
for j = 1:i
r(1,j) = r(2,j);
end
end
OutPut:
Enter lower limit, a: 0
Enter upper limit, b: pi
Enter no. of subintervals, n: 6
Romberg integration table:
0.00000000
1.57079633 2.09439510
1.89611890 2.00455975 1.99857073
1.97423160 2.00026917 1.99998313 2.00000555
1.99357034 2.00001659 1.99999975 2.00000002 1.99999999
1.99839336 2.00000103 2.00000000 2.00000000 2.00000000 2.00000000
>>





























No comments