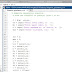
Adaptive Quadrature Algorithm using MATLAB (m file)
%
Adaptive quadrature algoritm
%
Find the integral of y=sin(x) from 0 to pi.
f = @(x)
sin(x);
aa = input('Enter
lower limit, a: ');
bb = input('Enter
upper limit, b: ');
n = input('Enter
maximum no. of levels, n: ');
eps = input('Enter
tolerance, tol: ');
cnt = 0;
app = 0;
i = 1;
tol = zeros(1,n);
a = zeros(1,n);
h = zeros(1,n);
fa = zeros(1,n);
fc = zeros(1,n);
fb = zeros(1,n);
s = zeros(1,n);
l = zeros(1,n);
fd = zeros(1,n);
fe = zeros(1,n);
v = zeros(1,7);
tol(i) = 10*eps;
a(i) = aa;
h(i) = 0.5*(bb-aa);
fa(i) = f(aa);
cnt = cnt+1;
fc(i) = f((aa+h(i)));
cnt = cnt+1;
fb(i) = f(bb);
cnt = cnt+1;
s(i) = h(i)*(fa(i)+4*fc(i)+fb(i))/3;
l(i) = 1;
while i > 0
fd = f((a(i)+0.5*h(i)));
cnt = cnt+1;
fe = f((a(i)+1.5*h(i)));
cnt = cnt+1;
s1 = h(i)*(fa(i)+4*fd+fc(i))/6;
s2 = h(i)*(fc(i)+4*fe+fb(i))/6;
v(1) = a(i);
v(2) = fa(i);
v(3) = fc(i);
v(4) = fb(i);
v(5) = h(i);
v(6) = tol(i);
v(7) = s(i);
lev = l(i);
i = i-1;
if abs(s1+s2-v(7)) < v(6)
app = app+(s1+s2);
else
if lev >= n
fprintf('Procedure
fails');
else
i = i+1;
a(i) = v(1)+v(5);
fa(i) = v(3);
fc(i) = fe;
fb(i) = v(4);
h(i) = 0.5*v(5);
tol(i) = 0.5*v(6);
s(i) = s2;
l(i) = lev+1;
i = i+1;
a(i) = v(1);
fa(i) = v(2);
fc(i) = fd;
fb(i) = v(3);
h(i) = h(i-1);
tol(i) = tol(i-1);
s(i) = s1;
l(i) = l(i-1);
end
end
end
fprintf('The
approximate integral is: %11.8f \n',
app);
OUTPUT:
>> Adaptive_quadrature_c
Enter lower limit, a: 0
Enter upper limit, b: pi
Enter maximum no. of levels, n: 6
Enter tolerance, tol: 0.001
The approximate integral is: 2.00026917
>>





























No comments