MATLAB Program for Sampling theorem and aliasing effect

Sampling:

 A continuous time signal can be processed by processing its samples through a discrete time system. For reconstructing the continuous time signal from its discrete time samples without any error, the signal should be sampled at a sufficient rate that is determined by the sampling theorem.

Nyquist Sampling Theorem:

 If a signal is band limited and its samples are taken at sufficient rate than those samples uniquely specify the signal and the signal can be reconstructed from those samples. The condition in which this is possible is known as Nyquist sampling theorem.

Aliasing:

 In reconstructing a signal from its samples, there is another practical difficulty. The sampling theorem was proved on the assumption that the signal x(t) is bandlimited. All practical signals are time limited, i.e., they are of finite duration. As a signal cannot be timelimited and bandlimited simultaneously.  

Sampling theorem and aliasing effect

clc

clear all;

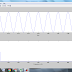
t=0:0.001:0.1;

Fs=1/0.001;

x =cos(2*pi*1100*t);

subplot(2,1,1);

plot(t,x);

xlabel('time');

ylabel('amplitude');

N=100;

for i=1:N

    F(i)=i*Fs/100;

end

subplot(2,1,2);

plot(F,abs(fft(x,N)));

xlabel('Frequency in Hz');

ylabel('Magnitude');

Output: